Biometrikus azonosítás felhasználása hiteles digitális aláírások előállítására

Orvos Péter <orvos@mit.bme.hu>

BME - Méréstechnika és Infromációs Rendszerek tsz.

Hornák Zoltán <hornak@mit.bme.hu>

BME - Méréstechnika és Információs Rendszerek tsz.

Selényi Endre Dr. <selenyi@mit.bme.hu>

BME - Méréstechnika és Információs Rendszerek tsz.

Összefoglaló

A jelenleg használatos digitális aláírási megoldások esetén, az aláíró személy azonosításában a leggyengébb láncszemet leggyakrabban az aláíró titkos kulcs és tulajdonosának összerendelése jelenti. Több kutatócsoport is felismerte a tényt, hogy a digitális aláírások előállítása során is szükséges a felhasználók biometrikus azonosítása, ám ennek megoldása több problémába ütközik. A továbbiakban olyan alternatívákat tekint át illetve elemez a cikk, amelyek elvárásaink alapján képesek a biometrikus mintából olyan digitális információt kinyerni, amely segítségével a titkos aláíró kulcsot rejtjelezni, illetve visszaállítani lehetséges. Ilyen módon egy hiteles aláírás nem csak az aláíró kulcs, mint birtok meglétét igazolja csupán, hanem azt is, hogy a kulcs tulajdonosa aktívan közreműködött az aláírás előállításában, hiszen az ő biometrikus azonosítása nélkül a titkos kulcs rejtve maradt volna. Az elméleti módszer gyakorlati megvalósítására két ujjlenyomat alapú azonosítást feltételező alternatíva is bemutatásra kerül.

Bevezető

A hétköznapi életben rengeteg helyen használjuk a hagyományos értelemben vett aláírásokat. Igazolják egyes dokumentumok hitelességét, vagy azt, hogy az aláíró elfogadja a dokumentumban foglaltakat.

A számítástechnika előretörésével fontossá vált, hogy a digitális világban is legyen megfelelője az “aláírásnak”, ennek biztosítására jött létre a nyilvános kulcsú titkosításon [1] és a PKI infrastruktúrán [2] alapuló digitális aláírás, amelyet napjainkban már egyre szélesebb körben használnak, sőt egyre több országban fogadják el hivatalosan is.

Az aláírás ellenőrizhetősége szempontjából elengedhetetlen az aláíró személy és az aláírt dokumentum megbízható összerendelése. Ez kriptográfiailag úgy oldható meg, hogy minden személyhez egy titkos és egy nyilvános kulcsot rendelnek: a nyilvános kulcsot ezután a PKI segítségével mindenki számára hozzáférhetővé teszik, míg a titkos kulcsot védett helyen tárolják. Ilyen formán egy megbízható Certificate Authority (CA) képes saját digitális aláírásával harmadik fél előtt igazolni a személyek nevének (Distinguished Name) és nyilvános kulcsainak összetartozását. Ha igazolt az aláíró személy és a nyilvános kulcsa közti kapcsolat, ezzel a kulccsal ellenőrizhető, hogy egy aláírás a megfelelő tikos kulcs felhasználásával készült-e. Ez a megoldás feltételezi, hogy a titkos kulcs csak az őt megillető személy birtokában lehet, vagyis az aláíró fél azonosítható a birtokában levő titkos kulcs segítségével. Mint ahogyan ezt az 1. ábra is szemlélteti, a létező technológiai megoldásokat figyelembe véve, mivel az alkalmazott kriptográfiai algoritmusok tetszőlegesen erőssé tehetők, a leggyengébb kapcsolat a titkos kulcs és az aláíró személy összerendelésénél található.

1. Aláíró azonosítása a jelenlegi PKI ajánlás szerint

Az implementációkban az aláíráshoz szükséges titkos kulcsot többnyire chip-kártyán tárolják, amely képes elvégezni a szükséges kódolásokat, míg magát a titkos kulcsot soha nem adja ki magából. Ennél kevésbé biztonságos megoldás, ha a számítógép merevlemezén található az aláírás elkészítéséhez szükséges titkos kulcsot tartalmazó fájl, hiszen azt így könnyen megszerezheti bárki, akinek sikerül valamilyen módon hozzáférnie a készülékhez.

Az eltulajdonítás útján történő károkozás illetve visszaélés lehetőségét chip-kártyák használata esetén mérsékelni lehet jelszó, vagy PIN kód segítségével úgy, hogy a kártya például nem hajlandó aláírást generálni addig, amíg a megfelelő jelszóval nem aktiválták. Ez esetben a felhasználó azonosítása birtok és tudás alapján, kombinált módon történik, ám még mindig nem biztos, hogy a megfelelő személy az, aki a kártyát felhasználja, hiszen a gyakorlat sajnos azt bizonyítja, hogy sokszor a felhasználókat is megtévesztik, így ők gyanútlanul, vagy tudtuk nélkül szolgáltatnak ki olyan titkos adatokat, mint az aláíró kulcsuk, jelszavuk vagy PIN kódjuk.

Ez az ismertetett PKI alapú azonosítás tehát több lépcsős. Az aláírás csak azt bizonyítja, hogy az aláírást készítő személy birtokában volt a megfelelő titkos kulcsnak [5].

Mivel a hagyományos értelemben vett aláírás nem más, mint az aláíró személy egy biometrikus paramétere, jogosan merül fel az igény, hogy a számítógépes aláírás is legyen képes biometrikusan azonosítani. Fontos megjegyezni, hogy az aláíró fél azonosítása során a későbbiekben ismertetett megoldásokban a biometrikus leolvasás eredményével kiegészíteni kívánjuk az eddig bemutatott tulajdon, illetve tudás alapú azonosítási módszereket, így is növelve a felhasználó és titkos kulcsa között az összerendelés erősségét.

A javasolt megoldás alapgondolata, hogy a leolvasott biometrikus paraméterből a chip-kártyán tárolt kiegészítő információk segítségével személyre jellemző bitsorozatot állítsunk elő, amely felhasználásával a titkos kulcs rejtjelezve tárolható. Természetesen nem célja munkánknak az, hogy egyetemesen használható egyedi személyazonosítókat állítsunk elő a biometrikus leolvasások eredményéből, sokkal inkább az, hogy a felhasználót azonosító kártya mások számára hasznavehetetlen legyen, hiszen abból a titkos kulcs csak a megfelelő biometrikus paraméter birtokában állítható vissza.

A következőkben ezt a módszert mutatom be, rávilágítva előnyeire, hátrányaira, valamint a megvalósítás során még megoldandó problémákra.

Háttér

1999-ben adta ki a Network Working Group a nyilvános kulcsú rejtjelezést infrastrukturálisan támogató Public Key Infrastructure (PKI) [2] szabványát. Ebben olyan megbízható szolgáltatókat (CA) definiáltak, amelyek tanúsítványok (certificate) kiállításával képesek igazolni a nyilvános kulcsok és tulajdonosaik összetartozását. A tanúsítványok adatszerkezetének felépítését az X.509 szabványnak megfelelően határozták meg.

A FIPS 1994-es FIPS-186 [3] (Digital Signature Standard - DSS) szabványa leírja a digitális aláírások általános szerkezeti felépítését, valamint előállításuknak és ellenőrzésüknek metodikáját. 1999-ben a DSS alapján az ETSI egy újabb szabványt készített [4] (Electronic Signature for Business Transactions). Ez utóbbi szabvány a digitális aláírások problémakörét a tranzakciós protokollok szempontjából célozza meg.

A FIPS-190 (Guideline for the Use of Advanced Authentication Technology) [5] szintén 1994-es ajánlás. Létrehozásának célja az volt, hogy összefoglalja a felhasználó azonosítására szolgáló különböző módszereket. Összefoglalja a három fő azonosítási módszert: tulajdon alapú, tudás alapú illetve biometrikus.

Biometrikus adatok eltárolása az aláírásban

A biometria és a digitális aláírások ötvözésének egyik módja a biometrikus adatok explicit beépítése a digitális aláírás szerkezetébe. Ilyen megoldás esetén az aláírás digitális része a már szabványosított úton készíthető el illetve ellenőrizhető, míg lehetőség van a biztonsági szint növelésére azáltal, hogy összevetik az aláírásban kódoltan tárolt biometrikus mintát egy, a megfelelő személytől vett hiteles mintával. Ujjlenyomatok használata esetén tehát az eljárás hasonlít arra, mint amikor valamely bűntett színhelyén talált mintákat összevetik a gyanúsított saját ujjlenyomatával, így bizonyítva, hogy jelen volt a helyszínen.

A módszer előnye, hogy rendkívül egyszerűen használható, és nem igényli újabb kriptográfiai módszerek kidolgozását; ellene szól viszont, hogy a személyazonosításra használt biometrikus paraméterek sok esetben személyes, illetve kiemelt személyes adatoknak számítanak, így azok nem csatolhatóak védelem nélkül az aláíráshoz. Olyan kódolásra van tehát szükség, amely elrejti a biometrikus információt illetéktelenek elől. Így viszont az aláírás ellenőrzője csak korlátozott ellenőrzést végezhet, és előfordulhat, hogy csak a bíróságon derül ki, hogy az aláírás érvénytelen. Ez viszont lehetőséget ad egy rosszindulatú aláírónak, hogy jónak tűnő, de mégis letagadható aláírást készítsen.

A biometrikus adatok védelme további két alapvető problémát vet fel. Elsősorban azt kell eldönteni, kik férhetnek hozzá a védett adatokhoz, valamint ki kell dolgozni egy olyan kódolási eljárást, amely úgy képes a biometrikus adatokat csatolni az aláírásokhoz, hogy ahhoz mindegyik illetékes személy hozzáférhessen, miközben másokkal szemben továbbra is megfelelő védelmet nyújtson.

Az illetékesség kérdéséhez biztosítani kell, hogy az aláírások leellenőrizhetőek legyenek, ám ezzel szemben áll, hogy az érzékeny adatokhoz nem férhet hozzá mindenki. Ezt az ellentmondást csakis egy biztonságtechnikailag jól megalapozott háttér-infrastruktúra, egy jól kialakított elektronikus közjegyzői rendszer lenne képes feloldani, amelyhez vitás esetben fordulhatnak a felek hitelesítési igényükkel. Egy ilyen infrastrukturális háttérrendszer kialakítása rendkívül költséges, és további technikai és felelősségbeli kérdéseket vet fel. A nehézségek ellenére egyre több ország mutat hajlandóságot ilyen infrastrukturális fejlesztések előírására, illetve a törvényes háttér megteremtésére [6]. Ennek a megoldásnak problémáit és különböző megoldási lehetőségeit, valamint a szükséges háttér-infrastruktúrát tárgyalja diplomamunkám [11].

Ami a biometrikus adatok kódolását illeti, szintén nehéz problémával állunk szemben, hiszen ha egy illetéktelen személynek sikerül kinyernie egy aláírásból a benne található biometrikus adatokat, akkor azt újabb, hamis aláírások előállítására használhatja fel. Ezt a veszélyt megnyugtató módon úgy lehetne csak kivédeni, ha a biometrikus paraméterek nem is lennének jelen az aláírásban, hanem az aláírás csak a megfelelő személy azonosításának megtörténtét bizonyítaná valamilyen más, indirekt módon, így már nem tartalmazva érzékeny információkat. Emellett szól az is, hogy a leolvasott paraméterek sokszor nagy adatmennyiséget képviselnek, amit ha kódolt állapotban is, de csatolni kellene az aláírásokhoz, ami főként alacsonyabb sávszélességű továbbítás esetén eredményezne megnövekedett továbbítási költséget.

Biometrikus kulcstárolás

Egy másik megoldás, hogy a leolvasott biometrikus adatokat az aláíráshoz csatolás helyett inkább arra használjuk fel, hogy a kódolt formában tárolt titkos kulcsot visszaállítsuk, és így felhasználhatóvá tegyük. Ilyen módon a titkos és nyilvános kulcsok használatának módja megmarad, ám a hiteles aláírás bizonyítja azt is, hogy tulajdonosa jelen volt, és aktívan közreműködött az aláírás elkészítésében, hiszen másképp nem állhatott rendelkezésre a titkos kulcs.

A módszer alapgondolata logikus, ám egy problémát még le kell küzdeni, mielőtt széles körben használhatóvá válna: szükség van egy algoritmusra, amely a biometrikus minta, és a kártyán tárolt információk segítségével képes előállítani egy bináris vektort, amely a kártya tulajdonosára jellemző. A probléma az, hogy a biometrikus paraméterek mérés eredményei, így mérési hibák torzíthatják azokat, míg a titkos kulcs visszanyeréséhez minden alkalommal bitről-bitre egyező vektor szükséges. Emiatt hibajavító mechanizmus beépítése szükséges, amely az adott biometrikus paraméternél használt személyazonosító eljárásokon, illetve azok hibakarakterisztikáján alapul. A következő fejezetekben ujjlenyomat alapú személyazonosításból kiindulva különböző módszerek kerülnek majd ismertetésre.

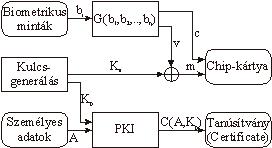
1. Kulcsgenerálás, valamint a chip-kártya biometrikus referenciamintákkal történő inicializálása

A 2. ábra szemlélteti azt a folyamatot, ahogyan a felhasználó aláíró kártyáját feltöltik a szükséges adatokkal. Ezek az adatok részben a felhasználó számára generált titkos (K_s) és nyilvános (K_p) kulcsokból, részben pedig a tőle hiteles személyazonosítást követően vett biometrikus referencia mintákból (b₁, b₂, .. , b_n) származnak. A “G” függvény elemzi a referencia-mintákat, és részben előállít egy, az adott személyre jellemző bináris vektort (v), részben pedig egy hibajavító kód által generált redundancia-vektort (c), amely a későbbiekben segít kiszűrni a biometrikus mérések hibáit. Végül a hibajavító információt, valamint a titkos kulcs és a személyre jellemző bináris vektor kombinációjával előállított master secret-et (m) védetten eltárolják a chip-kártyán, míg a nyilvános kulcsot a személy egyedi adataival együtt egy CA tanúsítványba foglalja (C(A,K_p)).

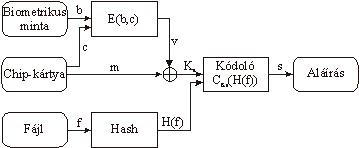
1. Aláírás előállítása a biometrikus paraméter leolvasásával

Az aláírások előállításának mechanizmusát szemlélteti a 3. ábra. Jól látható, hogy a jelenlegi algoritmus felépítése megmaradt, így az aláírt dokumentumból (f) egy hash lenyomatot (H(f)) képzünk, amit a felhasználó titkos kulcsával (K_s) kódolunk, és így kapjuk meg az aláírást (s). Az algoritmust mindössze ki kell egészíteni azzal a mechanizmussal, amely a leolvasott biometrikus jellemző (b), valamint a kártyán tárolt hibajavító információ segítségével előállítja a felhasználóra jellemző bináris vektort (v), amelynek a kártyán levő master secret-tel (m) vett kombinációjával minden aláíráskor egyedileg előállítja az aláíró kulcsot. Amennyiben nem a jogos tulajdonostól származó biometrikus minta kerül az algoritmus bemenetére, biztosítani kell, hogy csak nagyon kis valószínűséggel állhasson elő ugyanaz a bináris vektor a hibajavító függvény (E(b,c)) kimenetén, mint ami a jogos tulajdonoshoz tartozik.

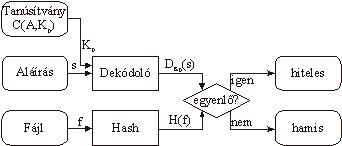
1. Biometrikusan előállított aláírás ellenőrzése

Mint ahogyan azt a 4. ábra is mutatja, az ilyen módon generált aláírás ellenőrzése pontosan ugyanolyan módon történik, mint a jelenlegi megoldások esetén: az aláíró fél tanúsítványából kinyert publikus kulccsal (K_p) dekódolni kell az aláírást (s), és megvizsgálni, hogy az így kapott érték megegyezik-e azzal, amit a dokumentum (f) alapján a hash függvény (H(f)) eredményként ad. Ha a két érték egyezik, az aláírás hiteles, különben pedig hamis, azaz vagy nem az írta alá, mint akinek a tanúsítványát használtuk, vagy az aláírást követően a dokumentum tartalma módosult. A hiteles aláírás azonban itt azt is igazolja, hogy a titkos kulcs jogos birtokosa jelen volt, és közreműködött az aláírás elkészítésében.

Ujjlenyomat alapú, minutiae pontokra épülő megoldás

Eddig általánosságban biometrikus azonosításról volt szó. A továbbiakban viszont az ujjlenyomat azonosítás konkrét módszerével fogunk csak foglalkozni.

Ujjlenyomat alapú azonosítás esetén az ujjbegy redőzetét vizsgáljuk. Ennek kitűntetett pontjai a minutiae pontok, amelyek a bőrredők elágazásainál, illetve végződéseinél találhatók.

A szakirodalomban több forrás is részletesen tárgyalja a leolvasott ujjlenyomat-képek előfeldolgozásának, valamint a minutiae pontok kinyerésének technikáit [7][8], amellyel terjedelmi okokból itt nem foglalkozunk.

A fellelhető algoritmusok alapvető célja két ujjlenyomatból származó ponthalmaz összehasonlítása, és annak eldöntése, hogy azok származhatnak-e egy személytől. Ehhez az szükséges, hogy az egyes pontokat megfeleltessék egymásnak a két halmazban. A megfeleltetést úgy valósítják meg, hogy pár sikeresen beazonosított pont, és a hozzájuk rendelt bőrredő futási irányának segítségével kiszámítják azt az eltolást és elforgatási szöget, amellyel a mintavételezett ponthalmaz áttranszformálható a referencia halmazba (5. ábra). Ezek után az egymással átfedésbe eső pontok összepárosíthatók, és az azonosság-vizsgálat elvégezhető.

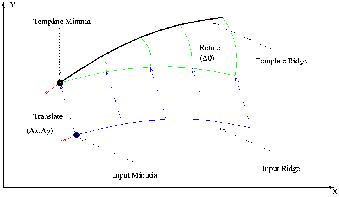
1. A minutiae ponthalmazok megfeleltetése szükséges transzformáció¹ [7]

Ez a módszer azonban kizárólag arra alkalmas, hogy két minutiae ponthalmazt összevessen, arra nem képes, hogy egy ponthalmazból olyan egzakt információt nyerjen ki, amely minden leolvasás esetén megegyezne, valamint összehasonlítási alap nélkül értelmezhető volna rajta a “mérési hiba” fogalma, illetve annak kijavítása, ami a mi módszerünk alkalmazásához elengedhetetlen. Ezért egy olyan módszer alapos vizsgálatát tűztük ki célul, amely működését tekintve követi a személyazonosítás módszertanát. Az elgondolás szerint a kártyán két ponthalmaz kerül eltárolásra: egy referencia-ponthalmaz, amely karakterisztikus része az adott személy ujjlenyomatának, így jól használható a fent leírt pont-transzformáció paramétereinek kiszámítására, valamint egy teszthalmaz, amely részben olyan pontokat tartalmaz, amelyek környezetében található minutiae pont, részben viszont olyan pontokat is, amelyek körül nem. Ilyen módon a 4. fejezetben definiált v vektor úgy épül fel, hogy minden bitjéhez tartozik egy tesztpont, és a bit értéke 1, amennyiben a leolvasott mintán volt a tesztpont környezetében minutiae pont, egyébként pedig 0.

A leolvasás pontatlansága miatt számítani lehet arra, hogy még a megfelelő személytől vett ujjlenyomat esetén is a minutiae pontok kis mértékben elmozdulva jelennek meg, egyes pontok nem kerülnek detektálásra, mások pedig megjelenhetnek a referenciamintákhoz képest. Ennél fogva tehát az előálló vektor bithibákat fog tartalmazni, hiszen előfordulhat, hogy egy tesztpont környezetében a referenciaminták alapján várnánk minutiae pontot, viszont mégsem találunk, vagy fordítva, nem várt pontok is megjelenhetnek. Várakozásunk szerint viszont az egy személytől származó minták esetén található olyan korlát (L_biterror), amelynél azonos személytől származó minták esetén nagy valószínűséggel kevesebb, míg különböző személyektől származó minták esetén várhatóan több bithiba lép fel az elvárt, személyre jellemző értékhez képest. Ez esetben ugyanis készíthető olyan hibajavító kód, amely L_biterror darab bithibát képes javítani, viszont ennél többet már nem, így a redundáns biteket a kártyán eltárolva elérhető, hogy a megfelelő személytől származó mintát helyes értékre javítsa a rendszer, míg a másoktól származókat helytelenekre. (A hibajavító kód szavai v és c konkatenációjával állnak elő.)

Ilyen megoldást feltételezve a felhasználó hibás azonosításának valószínűségét a következő képlet adja:

, (1)

ahol A kártyáját, és így a benne tárolt R_A referencia pontokat, T_A tesztpontokat, és m_A master secret-et használja B, akitől S_B mintát vettük le. Az m függvény a paraméterül kapott bináris vektor súlyát, azaz a benne levő 1 bitek számát határozza meg, az E a hibajavító függvény, míg a T a tesztpontok (T_A) alapján álltja elő a fent leírt bináris vektort. Ahhoz, hogy az A kártyájával K_sA kulcs álljon elő, szükséges, hogy mindkét személytől vett ujjlenyomat esetén azonos bináris vektor álljon elő (v_A=v_B).

Vizsgálni kell tehát annak statisztikus valószínűségét, hogy egy személytől származó karakterisztikus ponthalmaz előforduljon más emberek ujjlenyomatában is, valamint azt, hogy ilyen esetekben, mekkora a valószínűsége annak, hogy a tesztpontok kiértékelésekor a megengedett tévesztési határnál (L_biterror) kevesebb pontban kapunk az elvárttól eltérő eredményt. Ezek függvényében meg kell határozni a karakterisztikus ponthalmaz előírható számosságát, valamint a konzisztensen kiértékelhető tesztpontok, illetve a megengedhető hibák számát. Ez utóbbi paraméterek meghatározásánál figyelembe kell venni, hogy a jogos tulajdonost nagy valószínűséggel kell felismerni, míg a téves felismerés kockázatát minimalizálni kell.

Ujjlenyomat alapú, grafikus szűrőket alkalmazó megoldás

Sok reménnyel kecsegtet a grafikus Gábor-szűrőket alkalmazó FingerCode eljárás is [8], amelynek kidolgozói szintén az ujjlenyomatok összehasonlítását célozták meg, ám megoldásukban az eltárolt referencia (template) érték, amelyhez aztán a leolvasott mintát hasonlítják egy olyan kód, amelyen euklideszi távolságokkal definiálható a leolvasási pontatlanság. Algoritmusukkal az ujjlenyomatból egy 640 bájtos vektort állítanak elő, az összehasonlítás során pedig az eltérést a megfeleltethető értékek különbségnégyzeteinek összegével fogalmazzák meg:

(2)

A fenti képletben e a távolság, vagy más néven hiba, s_i értékek származnak az aktuális mintából, míg t_i értékek tartoznak az eltárolt referenciához. Az algoritmus működését a 6. ábra szemlélteti.

1. FingerCode használata ujjlenyomatok összehasonlítására² [10]

Az algoritmus először meghatározza az ujjlenyomat “középpontját”, vagyis azt a pontot, ahol a bőrredő rajzolata a legkisebb ívben görbül, valamint lokális szimmetria alapján egy irányvektort [10]. Ezek együtt meghatározzák a “reference frame”-et, amelyre a vizsgálat során használt szektorrácsot ráillesztik. Erre azért van szükség, hogy minden alkalommal hozzávetőleg azonos ujjlenyomat-szegmensek essenek az egyes szektorok területébe. A forrásmunkában beszámolnak kísérleti eredményekről is, amelyek igazolták, hogy a referencia keret meghatározásának hozzávetőleges, nem pontos módja nagyon kis mértékben befolyásolja a későbbi feldolgozás eredményét.

A szektorháló 5 gyűrűből, és gyűrűnként 16 szektorból áll. Mindegyikre lokális normalizálást hajtanak végre, majd 8 Gábor-szűrőn engedik keresztül a normalizált képet. A Gábor szűrők arra szolgálnak, hogy kiemeljék az ábrák egyes irányok menti változatosságát, míg elnyomják a merőleges irányú változatosságot. A szűrők 22,5°-os lépésekkel fedik le a lehetséges irányokat, így minden bőrredő, fusson az bármilyen irányba, több képen is kisebb vagy nagyobb dominanciával megjelenik. Szektorokhoz rendelt értékek ezután a (3) függvény segítségével számíthatók.

, (3)

ahol K_i az i. szektorban található képpontok száma, P_iq az i. szektor képpont értékeinek átlaga, F_iq(x,y) pedig a q fokkal definiált Gábor-szűrővel előállított kép i. szektorának x, y koordinátájú képpontjának értéke. Egy-egy V_iq érték azt jellemzi, hogy az i. szektorban milyen gyakorisággal fordulnak elő q irányba mutató bőrredő-részletek.

Az ujjlenyomatokhoz rendelt kódnak tehát a 160 különböző V_iq érték sora felel meg. Mivel ez elég sok redundanciát tartalmaz, valamint azért, mivel minden leolvasás során pontosan megegyező vektort szeretnénk kapni, nem szükséges ennyi adat használata. Amennyiben csökkentjük az egyes V_iq értékek kvantáltságát, az azonos személyhez tartozó minták esetén az értékek ingadozása csökkenthető, így elérhető, hogy a megengedhető tolerancia-szinthez az értékek maximum ±L_{code_tolerance} megváltozása tartozzon, amely a chip-kártyán tárolható hibajavító információ segítségével a felhasználás során eliminálható, és így minden alkalommal nagy valószínűséggel a jó aláíró kulcs áll majd elő (K_s). Ezzel szemben, ha valaki illetéktelenül használja a kártyát aláírásra, annak valószínűsége, hogy az ujjlenyomata alapján előálló redukált FingerCode megegyezzen az kártya tulajdonosáéval, minimális értéken tartható. A módszert publikálók tesztjei alapján a közel 100%-os helyes felismerési arányhoz mindössze 1% körüli hibás azonosítás tartozott, míg a gyakorlatilag 0%-os hibás felismerés esetén is közel 95%-ban volt sikeres az azonosítás. További teszteknek kell megválaszolniuk azt a kérdést, hogy a kód redukálása mennyire rontja le ezeket az eredményeket.

Következtetés

A digitális aláírások felhasználási köre egyre terjed, így szükséges az aláíró személy azonosságának minél megbízhatóbb bizonyítására. Mivel a jelenlegi megoldások alapvetően csak birtok, illetve korlátozottan tudás alapján azonosítják az aláírót, a védelem elviekben sem fokozható tovább, ezért csak a biometria bevonásával erősíthető a titkos aláíró kulcs, valamint tulajdonosának összerendelése.

A cikkben bemutatásra került két alapvető módszer a biometrikus felhasználó-azonosítás, valamint a digitális aláírás ötvözésére. Az egyik megoldás a biometrikus leolvasás eredményét kódolt formában csatolta az aláíráshoz, amelynek előnye, hogy nem igényli újabb kriptográfiai módszerek kidolgozását, hátránya viszont, hogy érzékeny információk nyilvános továbbításán alapul, és szükséges hozzá egy on-line elérhető elektronikus közjegyzői rendszer, amely képes a biometrikus adatok dekódolására és ellenőrzésére.

A másik módszer azon az ötleten alapul, hogy az aláírás elkészítéséhez szükséges titkos kulcsot csak részben tárolják el az aláíró eszközben (master secret – m), viszont a chip-kártyára hibajavító információ (c) is kerül, amely segítségével a biometrikus leolvasás (b) mérési hibáit kiküszöbölhetjük, és ezt a javított értéket (v) kombinálva (pl. bitenként XOR-olva) a master secret-tel áll elő a szükséges titkos kulcs (K_s). Ily módon a hiteles aláírás igazolja azt is, hogy a kártya tulajdonosa személyesen jelen volt és közreműködött az aláírás elkészítésében.

Ez utóbbi elgondolás problémás részletét az képezi, hogy amíg a kulcs visszaállításához minden alkalommal bitről-bitre egyező vektorra van szükség, addig a biometrikus paraméter leolvasása mindig zajjal terhelt, így elkerülhetetlen egy olyan algoritmus kidolgozása, amely képes a mérési hibák hatásait a jelenlegi összehasonlításokon alapuló módszerek felhasználásával eliminálni.

Két ilyen módszert is ismertettem. Az egyik esetben az ujjlenyomat pozícionálását referencia-pontok segítik, és azt vizsgáljuk, hogy a különböző tesztpontok kis környezetében található-e a leolvasott ujjlenyomaton minutiae pont, és az ilyen esetekben előforduló bithibákat javítja. Ez esetben a jogosulatlan használó két módon is felismerhető, mivel nagy valószínűséggel nem sikerül az ujjlenyomatára illeszteni a referencia ponthalmazt, illetve ha az illesztés mégis sikeres lenne, annak valószínűsége, hogy a hibajavítás után azonos bináris vektor álljon elő, várakozásaink szerint csekély, így a rossz aláíró kulcs használatával nem okozhat kárt a támadó.

A második módszer már az eredeti egyezőség-vizsgálathoz is egyfajta kódot definiál (FingerCode), amely kódok euklideszi távolságban képesek kifejezni az összehasonlított ujjlenyomatok között fennálló eltérőséget. A továbbiakban tesztekkel fogjuk meghatározni, hogy ezek a kódok milyen mértékben redukálhatóak úgy, hogy hibajavító kódolással kiegészítve a kártya tulajdonosától származó mintákra nagy valószínűséggel azonos eredményt adjanak, miközben a hibás azonosítás valószínűségét minimális értéken tartsuk.

Referenciák

1. RFC-2437, Network Working Group, B. Kaliski, J. Staddon, RSA Laboratories: “RSA Cryptography Specifications Version 2.0”, October 1998.

2. RFC2459, Network Working Group: “Internet X.509 Public Key Infrastructure Certificate and CRL Profile”, January 1999.

3. FIPS-186, NIST: “Digital Signature Standard (DSS)”, May 1994.

4. Internet Draft: ETSI ES 201 733 v1.1.3, European Telecommunications Standards Institute, SEC working group: “Electronic signature standardization for business transactions”, September 1999.

5. FIPS-190, Department of Commerce, NIST: “Guideline for the Use of Advanced Authentication Technology”, September 1994.

6. Katona Kálmán, Közlekedési, hírközlési és vízügyi miniszter; dr. Dávid Ibolya, Igazságügy-miniszter: “Előterjesztés a Kormány részére az elektronikus aláírás és irat szabályozásának koncepciójáról és az ezzel kapcsolatos szükséges intézkedésekről”, Budapest, 2000. január

7. MSU-CPS-96-43, Lin Hong, Anil K. Jain – Michigan State University, and Sharath Pankanti, Ruud Bolle – IBM T. J. Watson Research Center: “Identity Authentication Using Fingerprints”

8. Nalini K. Ratha, Shaoyun Chen, Anil K. Jain – Department of Computer Science, Michigan State University: “Adaptive Flow Orientation Based Feature Extraction in Fingerprint Domain”, February 12, 1995.

9. MSU-CPS-98-36, Anil K. Jain, Salil Prabhakar, Lin Hong – Michigan State University, and Sharath Pankanti – IBM T. J. Watson Research Center: “FingerCode: A Filterbank for Fingerprint Representation and Matching”

10. M. Kawagoe, A. Tojo: “Fingerprint Pattern Classification”; Pattern Recognition, Vol. 17, Nr. 3, 1984.

11. Orvos Péter – BME-MIRT: “Elektronikus aláírások háttér-infrastruktúrája” (diplomamunka), 2000. június; http://www.mit.bme.hu/~orvos/Diploma.pdf